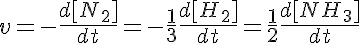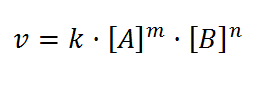Ecuaciones de tercer grado

Ecuaciones de tercer grado

Introducción Sin duda, una de las fórmulas más conocidas y usadas en Matemáticas es la que provee las soluciones de una ecuación de segundo grado. En cambio para las ecuaciones de tercer y cuarto grado tal procedimiento es prácticamente desconocido, si bien se sabe que ellas pueden resolverse mediante fórmulas del mismo estilo. Aparecen algunas referencias en textos de historia pero en la bibliografía de uso general no se encuentran explicaciones sencillas ni mucho menos ejemplos o ejercicios. En mi opinión, es necesario que uno conozca los métodos de solución existentes para resolver una ecuación general de tercer grado. Así que en éste capítulo, encontrará el lector los métodos clásicos de Cardano-Tartaglia, como también los métodos de Euler y Lagrange, entre otros métodos innovadores que permiten resolver una ecuación cúbica de forma general. Hablar de ecuaciones cúbicas, es remontarnos a la historia en los tiempos árabes, donde destaca Omar Khayyam (1050-1123), quien consideraba imposible dar solución de tipo aritmético a las ecuaciones cúbicas y presenta únicamente soluciones geométricas mediante intersecciones de cónicas para resolverlas.

 Lo más relevante de Omar Khayyam fue que generalizó el método para cubrir todas las ecuaciones que tengan alguna raíz positiva. Él se da cuenta que estas ecuaciones no pueden resolverse por medio de la geometría plana, es decir utilizando únicamente regla y compás sino que requiere las secciones cónicas. En notación algebraica, el planteamiento de Omar Khayyam se reduce a remplazar en la ecuación + + + = 0, por 2 de donde 2 + 2 + + = 0 que es la ecuación de una hipérbola, mientras que = 2 representa una parábola. Las abscisas para las cuales la hipérbola y la parábola se cortan serán las raíces de la ecuación cúbica. Durante los siglos XV y XVI, habiéndose determinado la solución de las ecuaciones cuadráticas, se plantean problemas que generan ecuaciones cúbicas. Scipione dal Ferro (1465-1526), profesor de matemáticas de Bologna, resolvió ecuaciones particulares del tipo + = aunque no publicó su método. Hacia 1510 le confía su secreto a Antonio María Fior quien años más tarde reta a Niccoló Fontana de Brescia (1499-1557) conocido como “Tartaglia” a resolver treinta ecuaciones de grado tres. Tartaglia resolvió las treinta ecuaciones en donde se incluían algunas de la forma + = con y positivos e incluso de la forma + = y cuyos procedimientos eran desconocidos para Scipione dal Ferro. Gerolamo Cardano, médico renacentista, destacado por sus trabajos en álgebra, publica hacia 1545 y rompiendo una promesa a Tartaglia, su solución para la ecuación + = en su libro Ars Magna. Tartaglia había revelado a Cardano su método en forma de verso, luego de una gran presión por parte de éste. El verso traducido al español es el siguiente: Cuando está el cubo con las cosas preso Y se iguala a algún número discreto Busca otras dos que difieran en eso Después tú harás esto que te espeto Que su producto sea igual al tercio cubo de la cosa neta. En realidad Tartaglia resuelve ecuaciones de los tres tipos siguientes: + = , + = y = + . De la ecuación cúbica + + + = 0, en la época de Cardano se consideraba tantos tipos como posibilidades para los signos positivos y negativos de los coeficientes. Dado el carácter geométrico que se le asignaba a toda expresión algebraica el número negativo no tenía sentido en el espacio físico. Como por ejemplo determinar un cuadrado de magnitud negativa o un volumen negativo de un cuerpo tridimensional. Cardano y su discípulo Ferrari, comprueban posteriormente, que el método de Tartaglia y de Antonio Fior son los mismos e incluso que algunas publicaciones de Tartaglia, eran traducciones de la obra de Arquímedes copiado de Guillermo de Moerbecke. Fiore sólo sabía resolver ecuaciones cúbicas incompletas del tipo + + = 0, pero Cardano había resuelto ecuaciones como: + + = 0 reduciéndolo al caso anterior por medio de una sustitución.

Método de Cardano-Tartaglia. En esta sección, deduciremos la fórmula para resolver la ecuación de tercer grado en forma general, usando algunos aspectos de las ideas de Cardano y Tartaglia. Consideremos la ecuación general de tercer grado: + + + = 0 … (1) donde , y son números reales. Es posible, mediante una Transformación de Tschirnhaus, eliminar el término cuadrático de la ecuación (1). Al utilizar la resultante para eliminar el término cuadrático, se llega a: = − … (2) Por lo tanto la ecuación (1) puede ser transformada de la siguiente manera: + + = 0 … (3) donde = − = − + A esta ecuación se le conoce como “ecuación cúbica reducida”. La ecuación (3) es más fácil de utilizar que la ecuación (1). Se puede proponer que la solución de (3) sea la suma de dos números y , es decir: = + … (4) Al sustituir (4) en (3), se obtiene: + + ( + )(3 + ) + = 0 … (5) Se observa que para que se cumpla la igualdad en (5), debe suceder que: + = − = − … (6)

 Al resolver el sistema de ecuaciones (6), se llega a una ecuación cuadrática: ( ) + ( ) − = 0 … (7) La ecuación (7) puede ser resuelta por la fórmula de Bháskara, por lo que: = − ± + … (8) De igual manera, se tiene que: = − ± + … (9) Es claro que para satisfacer el sistema de ecuaciones (6), se debe de cumplir que: = − 2 + √∆ = − 2 − √∆ donde ∆= + Por lo tanto, hemos encontrado una raíz de la ecuación cúbica. Al sustituir estos valores en (4): = − + √∆ + − − √∆ … (10) A la cantidad ∆ se le conoce como el discriminante de la ecuación cúbica reducida. Finalmente, para encontrar , se hace uso de (2): = − 3 + − 2 + √∆ + − 2 − √∆ Este resultado es la llamada “fórmula de Cardano-Tartaglia”, para resolver una ecuación cúbica en forma general. Al analizar un poco la fórmula de Cardano-Tartaglia, existen dos dilemas y esto es algo que no pudo resolver Cardano ni Tartaglia.

¿Cómo calcular las otras dos raíces de la ecuación cúbica? ¿Qué pasa si el discriminante ∆ es menor a cero? Recordemos que en aquella época, aún no se descubrían los números complejos. 

Por esta razón, Cardano no supo qué hacer cuando ∆< 0, por lo que a éste caso, le llamó el caso irreducible. Así como en el caso de una ecuación cuadrática, su discriminante nos da información detallada del tipo de raíces que podemos tener, lo mismo sucede para una ecuación cúbica: su discriminante nos dirá cómo serán las raíces. Entonces, conviene enunciar el siguiente teorema: Teorema 2.1.a Consideremos una ecuación cúbica + + + = 0 con coeficientes reales. Entonces: a) Si ∆= 0 todas sus raíces son reales y al menos dos de ellas son iguales. b) Si ∆> 0 la ecuación tiene una raíz real y dos son complejas. c) Si ∆< 0 la ecuación tiene tres raíces reales simples. donde ∆= + En algunos artículos, podemos encontrar que el discriminante es definido de manera distinta, al presentado aquí. Esto se debe a la razón siguiente: el discriminante de la ecuación cúbica, de acuerdo con el capítulo anterior, está definido por la siguiente expresión: = ( , ´) (−1) ( ) De ahora en adelante, se usará la letra al discriminante de una ecuación polinómica definido por la expresión anterior. Si uno calcula el discriminante por medio de esta expresión, se obtiene que: = −4 − 27 Esta expresión no se parece en nada a ∆= + . 

Esto puede causar algo de confusión. Hay que aclarar que las dos expresiones son válidas; el detalle está en que hay que definir una relación que conjunte ambas expresiones. Entonces, podemos definir que: = −108 ∆ Esto permitirá relacionar ambos discriminantes. Ambas expresiones son correctas. Todo lo anterior que hemos visto es válido y podemos usar la expresión anterior para expresar la solución de en términos de : = − 3 + − 2 + − 108 + − 2 − − 108 Al simplificar la solución anterior, nos queda: = − + − 27 2 + 3 2 √−3 + − 27 2 − 3 2 √−3 3 Ambas expresiones de nos darán el mismo resultado. Entonces, de acuerdo a esto, podemos enunciar el siguiente teorema: Teorema 2.1.b Consideremos una ecuación cúbica + + + = 0 con coeficientes reales. Entonces: a) Si = 0 todas sus raíces son reales y al menos dos de ellas son iguales. b) Si < 0 la ecuación tiene una raíz real y dos son complejas. c) Si > 0 la ecuación tiene tres raíces reales simples. donde = −4 − 27 Tanto el teorema 2.1.a como 2.1.b son válidos. Si usamos ∆, aplicamos el teorema 2.1.a y si usamos , aplicamos el teorema 2.1.b. La mayoría de libros y artículos utilizan el teorema 2.1.a, por ser más simple la expresión para calcular . Ahora vamos a analizar una de las preguntas pendientes que no pudo resolver Cardano. ¿Cómo calcular las otras dos raíces de la ecuación cúbica?

Un método para poder encontrar las otras dos raíces faltantes de la ecuación cúbica es el utilizar división sintética a la ecuación cúbica reducida + + = 0. Al realizar esto, nos queda la siguiente ecuación cuadrática: + + ( + ) = 0 … (11) donde = − 2 + √∆ + − 2 − √∆ Al resolver (11) por la fórmula de Bháskara: , = ± … (12) Es posible escribir de otra manera la solución (12), mediante manipuleo algebraico. Sea = = − 2 + √∆ + − 2 − √∆ entonces , = ± = − ± √ + … (13) Al calcular , se tiene que = − 2 + √∆ + − 2 − √∆ + 2 4 − 27 + 4 = − + √∆ + − − √∆ − … (14) Ahora sea: = − + √∆ − − − √∆ … (15)

De igual manera, será: = − + √∆ + − − √∆ + … (16) De las expresiones (14) y (16), se obtiene que: = + … (17) Por lo tanto, de acuerdo con (13), las raíces , se pueden expresar como: , = − 2 ± √3 2 Por lo tanto, las otras dos raíces serán: , = − 3 − 2 ± √3 2 De esta expresión, se observa que efectivamente si y son cantidades reales, dos raíces de la ecuación cúbica serán números complejos. Ahora veamos cómo resolver la ecuación cúbica cuando el discriminante ∆ es menor a cero; es decir, analicemos el caso irreducible. En el libro Ars Magna, de Cardano, se analiza la siguiente ecuación cúbica: − 15 − 4 = 0 Al aplicar la fórmula de Cardano-Tartaglia, se obtiene que: = 2 + √−121 + 2 − √−121 Cardano no supo qué hacer con este tipo de expresiones. Fue Rafael Bombelli (1526- 1572) el primer matemático que calculó una raíz cúbica compleja. Bombelli hace lo siguiente: 2 + √−121 = 2 + 121(−1) = 2 + 11√−1

Relación entre posición velocidad y aceleración

Relación entre posición velocidad y aceleración

Objetivos

Estudiar el movimiento como un cambio continuo de posición respecto al tiempo a lo largo de una trayectoria.

Fundamento teórico

La posición de una partícula puede ser determinada por sus proyecciones sobre los tres ejes de un sistema de coordenadas rectangulares. Cuando la partícula se mueve en el espacio sobre una trayectoria cualquiera, sus proyecciones se desplazan en línea recta a lo largo de los tres ejes. El movimiento real puede reconstruirse a partir de los movimientos de estas tres proyecciones y asi estudiar el movimiento de un cuerpo sobre una línea recta o en movimiento rectilíneo.

La aceleración instantánea, constante en cualquier punto en un movimiento rectilíneo uniformemente acelerado es:

Esta ecuación queda representada por una parábola en la grafica x vs t. La pendiente de la tangente en cualquiera de los puntos de la curva es igual a la velocidad v en el instante t.

Experimento

• A. materiales :

• Carril de aire
• Sensor de movimiento
• Hilo o cuerda
• Masas
• 01 móvil
• Una computadora Pentium 3
• Interface PASCO 750

Procedimiento

• a. Movimiento rectilíneo uniforme (M.R.U.)

I. Conecte la interfase a la computadora y a su fuente de alimentación y enciéndalo, luego encienda la computadora. Active el programa Data estudio que controla la interfase y realice las conexiones necesarias en el programa para obtener datos experimentales gráficamente y obtenga todas las variables experimentales a partir de la información obtenida por él. Coloque el sensor de movimiento a una distancia mayor de 40cm. del carrito.

II. Obtenga las graficas x vs t y v vs t y analice una trayectoria.

• b. Movimiento rectilíneo uniformemente variado (M.R.U.V.)

I. Arme el esquema experimental y coloque un extremo del carril el sensor de movimiento conectándolo a la interfase. Conecte la interfase a la computadora y a su fuente y a su fuente de alimentación y enciéndalo, luego encienda la computadora. Active el programa Data estudio que contrala la interfase y realice las conexiones necesarias en el programa para obtener datos empleando el sensor de movimiento: Active una ventana para obtener los datos experimentales gráficamente determine todas las variables experimentales a partir de la información obtenida por el sensor de movimiento.

II. Realice una primera toma de datos con el profesor para definir de manera precisa la región de análisis y las condiciones iniciales del experimento.

Análisis

• a. M.R.U.

1. Del grafico obtenido de x vs t y v vs t. Determine la velocidad a la que se mueve el móvil. Para ello realice un ajuste por mínimos cuadrados de la grafica x vs t. Determine la ecuación del movimiento. Para comparar sus resultados determine el valor medio de la velocidad de la grafica v vs t con el valor de la pendiente obtenida de la grafica x vs t.

Reporte sus resultados en la tabla 1.

Tabla 1

• b. M.R.U.V.

2. Del grafico obtenido de v vs t, determine la aceleración (a) y la velocidad inicial (vo) a la que se mueve el móvil. Para ello realice un ajuste por mínimos cuadrados de la grafica v vs t.

3. Para comparar sus resultados realice un ajuste de la grafica x vs t empleando un polinomio de segundo orden. De este análisis usted debe determinar xo, vo y a. Compare sus resultados con los obtenidos en el paso anterior. Determine las ecuaciones del movimiento y registrelos en la tabla 2.

Tabla 2

Cuestionario

• 1. ¿Cómo se pueden manejar los datos de x vs t para graficar una recta (linealizarla)?

Para linealizarla hay que hallar por mínimos cuadrados los valores de m y b y llevar la ecuación cuadrática de papel milimetrado al papel logarítmico y también hallar la ecuación respectiva.

• 2. ¿Cómo modificaría el experimento para que la fuerza neta dependa del tiempo?

Para que todo dependa del tiempo, lo derivaría en un punto dado, ya que al derivar todo estaría en función de tiempo (la aceleración y la velocidad). Geométricamente hablando, para derivar un punto en la grafica debemos hallar la tangente.

• 3. Si a = 0, grafique v vs t y explique.

Como podemos observar, cuando no hay aceleración la velocidad se mantiene constante y por teoría sabemos que el área bajo la grafica se halla por v por t y por no presentar aceleración, el resultado es el espacio recorrido.

Cómo funciona el velocímetro en un carro?

Los velocímetros tradicionales están controlados por un cable recubierto que es torsionado por un conjunto de pequeñas ruedas dentadas en el sistema de transmisión.

La forma más común de un velocímetro depende de la interacción de un pequeño imán fijado al cable con una pequeña pieza de aluminio con forma de dedal fijada al eje del indicador. A media que el imán rota cerca del dedal, los cambios en el campo magnético inducen corriente en el dedal, que produce a su vez un nuevo campo magnético. El efecto es que el imán arrastra al dedal—así como al indicador—en la dirección de su rotación sin conexión mecánica entre ellos.

El eje del puntero es impulsado hacia el cero por un pequeño muelle. El par de torsión en el dedal se incrementa con la velocidad de la rotación del imán (que está controlada por la transmisión del vehículo). Así que un incremento de la velocidad del coche hace que el dedal rote y que el indicador gire en el sentido contrario al muelle. Cuando el par de torsión producido por las corrientes inducidas iguala al del muelle del indicador éste se detiene apuntando en la dirección adecuada, que corresponde a una cifra en la rueda indicadora.

El muelle se calibra de forma que una determinada velocidad de revolución del cable corresponde a una velocidad especifica en el velocímetro. Este calibrado debe de realizarse teniendo en cuenta muchos factores, incluyendo las proporciones de las ruedas dentadas que controlan al cable flexible, la tasa del diferencial y el diámetro de los neumáticos. El mecanismo del velocímetro a menudo viene acompañado de un odómetro y de un pequeño interruptor que envía pulsos a la computadora del vehículo.

Otra forma de velocímetro se basa en la interacción entre un reloj de precisión y un pulsador mecánico controlado por la transmisión del vehículo. El mecanismo del reloj impulsa al indicador hacia cero, mientras que el pulsador controlado por el vehículo lo empuja hacia la indicación máxima. La posición del indicador refleja la relación entre las salidas de los dos mecanismos

¿Cómo miden sus velocidades los aviones?

El indicador de velocidad aerodinámica o anemómetro, mide la velocidad del avión expresada en nudos, con respecto al aire que se mueve alrededor. El indicador de velocidad aeródinamica contiene arcos coloreados en los extremos mezclados con los números que nos indican lo siguiente:

• Arco blanco: desde Vso hasta Vfe. Este arco blanco está en las velocidades bajas o lentas del avión, indica las velocidades a las que se puede operar con los flaps y las velocidades máximas a que se puede, si se tienen los flaps extendidos y pasas del arco blanco, se podrían dañar los flaps.
• Arco verde: desde Vs1 hasta Vno. Este arco verde está en las velocidades crucero del avión, son las velocidades que suele desarrollar el avión gran parte del vuelo y además en caso de turbulencias el avión no se daña.
• Arco amarillo: desde Vno hasta Vne. Este arco está en las velocidades altas del avión, hay que tener bastante precaución ya que sólo se puede llegar a esta velocidad cuando no hay turbulencias ni tampoco se pueden realizar maniobras bruscas con el avión porque sufriría algún dañoestructural.
• Línea roja: solo ocupa una línea (Vne). Esta línea está en las velocidades máximas a las que el avión puede desarrollar, no se debe llegar ni pasar de esta línea ya que el avión se daña con facilidad.

El indicador de velocidad vertical o VSI, indica si el avión está ascendiendo, descendiendo o va nivelado y la velocidad vertical a la que asciende o desciende generalmente en pies por minuto (f.p.m). Si la manecilla indica cero, el avión está nivelado, si está por encima del cero entonces está ascendiendo y si está por abajo de cero, entonces el avión desciende. A partir de esta información, se pueden mirar los números que indican la velocidad de ascenso y descenso.

¿Cuál es el procedimiento que emplea el radar de la policía para medir la velocidad de los automóviles?

Un radar de control de velocidad o pistola de velocidad es una pequeña unidad de radar Doppler usada para detectar la velocidad de objetos, especialmente camiones y automóviles con el propósito de regular el tránsito. Este radar no proporciona información sobre la posición del objeto. Emplea el principio del efecto Doppler aplicado a haces de radar para medir la velocidad de objetos a los que se apunta. Estas pistolas radar pueden ser manuales o montadas en un vehículo.

La mayoría de las pistolas radar operan en las bandas X, K, Ka, banda IR (infrarroja), y (en Europa) Ku. Otra tecnología alternativa, LIDAR, usa luz pulsada.

Las pistolas radar son, en su más simple forma, un transceptor de radio: envían una señal de radio, y luego recibe la misma señal que se ha reflejado en un blanco. La frecuencia de radar es diferente cuando retorna, y esas diferencias pueden calcularse dando la velocidad del objeto en cuestión.

Su haz de radar es similar al haz de luz que se expande con la distancia a medida que la señal de origen se incrementa, y algunos reflejos del haz desde el objeto vuelve a la pistola, y ésta usa el efecto Doppler para calcular su velocidad. Usando la comparación del cambio de frecuencia entre lo enviado y lo recibido se detecta su velocidad.

Todas las bandas de radar obran de diferente manera; operando en diferentes frecuencias. Las pistolas de banda X son las menos usadas, porque su haz es fuerte y fácilmente detectable. Además, muchos portones automáticos utilizan ondas de radio en la banda X y pueden posiblemente afectar las lecturas de las pistolas radar. Así resulta que las bandas K y Ka son las más usadas comunmente por la autoridad policial.

Haga una descripción del funcionamiento del radar y el sonar

El radar emite señales de radiofrecuencia y el sonar, que puede usarse como medio de localización acústica, emite impulsos sonoros. De hecho, la localización acústica se usó en aire antes que el radar, siendo aún de aplicación el SODAR (la exploración vertical aérea con sonar) para la investigaciónatmosférica.

El funcionamiento del sonar se ve afectado por las variaciones en la velocidad del sonido, especialmente en el plano vertical. El sonido viaja más lentamente en el agua dulce que en la salada. En cualquier agua la velocidad del sonido viene dada por el módulo de elasticidad y la densidad de masa.

El funcionamiento del radar se basa en emitir un impulso de radio, que se refleja en el objetivo y se recibe típicamente en la misma posición del emisor. A partir de este "eco" se puede extraer gran cantidad de información. El uso de ondas electromagnéticas permite detectar objetos más allá del rango de otro tipo de emisiones (luz visible, sonido, etc.)

¿Puede un cuerpo tener velocidad cero y, a pesar de eso, estar acelerándose? Justifique su respuesta

Como vemos en el grafico, el móvil no presenta velocidad en ese punto pero si presenta aceleración normal debido a que se mueve en una circunferencia de radio constante.

También podemos citar el caso en que soltamos un cuerpo desde una distancia h del suelo, en ese caso el cuerpo no tiene velocidad inicial pero si tiene aceleración, la de la gravedad.

Conclusiones

Después de haber realizado los experimentos correspondientes a la velocidad y aceleración de un móvil se ha llegado a las siguientes conclusiones:

• Si queremos que la aceleración y velocidad de un móvil este en función del tiempo solamente, debemos derivarlo.
• Un cuerpo puede tener aceleración a pesar de no tener velocidad.
• La aceleración en la grafica de v vs t es la pendiente siempre y cuando la velocidad no sea constante.

Ecuacion de la aceleracion

           Ecuacion de la aceleracion

1. La aceleración es la tasa de variación de la velocidad de un objeto cuando este se mueve.^[1]Si un objeto mantiene una velocidad constante, no estará acelerando. La aceleración solo ocurre cuando su velocidad cambia. Si esta varía a una tasa constante, el objeto se estará moviendo con aceleración constante.^[2] Puedes calcular la tasa de aceleración, que se mide en metros por segundo al cuadrado, en base al tiempo que le toma pasar de una velocidad a otra o a una fuerza que se aplica sobre el objeto.
2. 
3. Define la Segunda Ley de Newton. La Segunda Ley de Newton de la dinámica afirma que cuando las fuerzas que actúan sobre un objeto se desequilibran, este acelerará. La aceleración dependerá de las fuerzas netas que actúan sobre el objeto y su masa.^[6] Si utilizas esta ley, la aceleración se puede calcular cuando una fuerza conocida actúa sobre un objeto de masa conocida.

   • La ley de Newton se puede representar con la siguiente ecuación F_neta = m x a, donde F_neta es la fuerza total que actúa sobre el objeto, m es la masa del objeto y a es su aceleración.
   • Cuando utilices esta ecuación, las unidades deben estar expresadas en el sistema métrico. Usa kilogramos (kg) para la masa, newtons (N) para la fuerza y metros por segundo al cuadrado (m/s²) para la aceleración.
4. 
   2
   Encuentra la masa del objeto. Para encontrar la masa de un objeto, simplemente colócalo en una balanza y la tendrás expresada en gramos. Si tu objeto es muy grande, tal vez tengas que encontrar una referencia que te proporcione su masa. Es probable que en este caso la masa esté en kilogramos (kg).

   • Para esta ecuación, expresa la masa en kilogramos. Si esta está expresada en gramos, solo divídela entre 1000 para convertirla.
5. 
   3
   Calcula la fuerza neta que actúa sobre tu objeto. Esta es una fuerza sin equilibrio. Si tienes dos fuerzas opuestas y una es mayor que la otra, tendrás una fuerza neta en la dirección de la mayor.^[7] La aceleración se da cuando una fuerza desequilibrada actúa sobre un objeto, lo que provoca que cambie de velocidad en dirección a la fuerza que lo está empujando o lo jalando.

   • Por ejemplo, digamos que tu hermano mayor y tú están jugando al tira y afloja. Tú estás tirando de la cuerda hacia la izquierda con una fuerza de 5 newtons mientras tu hermano la tira en dirección opuesta con una fuerza de 7 newtons. La fuerza neta aplicada sobre la cuerda es de 2 newtons hacia la derecha, en dirección a tu hermano.
   • Para entender adecuadamente las unidades, debes saber que 1 newton (N) es igual a 1 kilogramo-metro/segundo al cuadrado (kg-m/s²).^[8]
6. 
   4
   Reacomoda la ecuación F = ma para encontrar la aceleración. Para ello puedes alterar esta fórmula dividiendo ambos lados entre la masa; de modo que a = F/m. Para encontrar la aceleración, solo tienes que dividir la fuerza entre la masa del objeto que se acelera.

   • La fuerza es directamente proporcional a la aceleración, lo que quiere decir que una fuerza mayor provocará una aceleración también mayor.
   • La masa es indirectamente proporcional a la aceleración, lo que quiere decir que con una masa mayor, la aceleración disminuirá.
7. 
   5
   Utiliza la fórmula para encontrar la aceleración. Esta es igual a la fuerza neta que actúa sobre un objeto dividida entre su masa. Una vez que hayas establecido los valores de tus variables, resuelve una división simple para encontrar la aceleración del objeto.

   • Por ejemplo, una fuerza de 10 newtons actúa de manera uniforme en una masa de 2 kilogramos. ¿Cuál es la aceleración del objeto?
   • a = F/m = 10/2 = 5 m/s²

Método

3

Verificar lo que has entendido

1. 1
   La dirección de la aceleración. El concepto de aceleración en física no siempre es igual al que utilizaríamos cotidianamente. Toda aceleración tiene una dirección que normalmente se expresa en una cifra positiva si es hacia la DERECHA o ARRIBA y negativa si es hacia la IZQUIERDA o ABAJO. Fíjate si tu respuesta tiene sentido en base a este desglose:

   Conducta del auto	¿Cómo cambia la velocidad?	Dirección de la aceleración
   El conductor va a la derecha (+) presiona el acelerador.	+ → ++ (más positivo)	positivo
   El conductor va a la derecha (+) presiona el freno.	++ → + (menos positivo)	negativo
   El conductor va a la izquierda (-) presiona el acelerador.	- → -- (más negativo)	negativo
   El conductor va a la izquierda (-) presiona el freno.	-- → - (menos negativo)	positivo
   El conductor va a una velocidad constante.	se mantiene igual	la aceleración es cero
2. 
   2
   La dirección de la fuerza. Recuerda que una fuerza solo provoca una aceleración en la dirección de la fuerza. Algunos problemas podrían engañarte con valores irrelevantes.

   • Problema de ejemplo: un barco de juguete con una masa de 10 kg acelera hacia el norte a 2 m/s². Un viento que sopla hacia el este ejerce una fuerza de 100 newtons sobre el barco. ¿Cuál es su nueva aceleración hacia el norte?
   • Solución: como la fuerza es perpendicular a la dirección del movimiento, esta no causa ningún efecto en el movimiento hacia dicha dirección. El bote continúa acelerando hacia el norte a 2 m/s².
3. 
   3
   Fuerza neta. Si más de una fuerza actúa sobre un objeto, combínalas en una fuerza neta antes de calcular la aceleración. Si tienes un problema en dos dimensiones, este será parecido al que te presentamos:

   • Problema de ejemplo: April está tirando de un contenedor de 400 kg hacia la derecha con una fuerza de 150 newtons. Bob está a la izquierda de dicho contendor, empujándolo con una fuerza de 200 newtons. Un viento que sopla hacia la izquierda ejerce una fuerza de 10 newtons. ¿Cuál es la aceleración del contenedor?
   • Solución: este problema utiliza un lenguaje engañoso para confundirte. Dibuja un diagrama y verás que las fuerzas son de 150 newtons a la derecha, 200 newtons a la derecha y 10 newtons a la izquierda. Si la "derecha" es la dirección positiva, la fuerza neta es de 150 + 200 - 10 = 340 newtons. Aceleración = F / m = 340 newtons / 400 kg = 0,85 m/s².

          Ecuación de velocidad

En el punto anterior hemos definido la velocidad instantánea como un límite de un cociente entre la variación de la concentración de los reactivos en un tiempo determinado cuando este tiempo tiende a cero. Es fácil ver (con conocimientos básicos de matemáticas) que esta relación es justamente la derivada de la concentración respecto del tiempo:

Si recuerdas la interpretación geométrica de la derivada sabrás que la pendiente de la recta tangente a la curva en un punto es igual a la derivada de la función en ese punto.

Supongamos que estudiamos la reacción de formación del amoníaco:

Si nos fijamos en la variación en la concentración de uno de los reactivos (el nitrógeno), podemos escribir la expresión de la velocidad instantánea del siguiente modo:

El signo negativo significa que el reactivo está desapareciendo.

Pero esta misma velocidad la podemos escribir en función del resto de sustancias intervinientes en la reacción. Si tenemos en cuenta que por cada molécula de nitrógeno desaparecen 3 de hidrógeno, también será cierto que la velocidad de desaparición del hidrógeno es tres veces superior a la del nitrógeno, por tanto:

Y por la misma razón, también podemos escribir la ecuación anterior en función de las variaciones de concentración de los productos:

En el laboratorio, la velocidad de una reacción se calcula midiendo la concentración de alguna de las sustancias intervinientes en diferentes tiempos. Una vez llevados los valores a una gráfica, podemos calcular la pendiente de la tangente en diferentes puntos para conocer la velocidad instantánea en cada momento.

De todas las variables que afectan a la velocidad de reacción, normalmente se suele hacer más hincapié en las concentraciones de las sustancias que toman parte en la reacción. Si se mantienen constantes variables como la temperatura, la presión y otras, entonces se puede determinar experimentalmente que la velocidad de una reacción es una función simple de dichas concentraciones. Experimentalmente, se puede comprobar que, en la mayoría de los casos, la velocidad es directamente proporcional al producto de determinadas potencias enteras de las concentraciones:v=k

 ⋅]

α

donde 

α

, 

β

, 

γ

, ... son constantes (habitualmente números enteros) y k

 es una constante de proporcionalidad que denominaremos constante de velocidad específica. Los exponentes de las concentraciones de cada especie que aparecen en esta ecuación se denominan órden de reacción respecto a la especie dada. Es decir, que según la expresión que hemos escrito, la reacción es de orden α

 respecto a la especie A

, de orden 

β

 respecto a B

, y así sucesivamente. El orden total de la reacción es la suma de los órdenes respecto a cada una de las especies que aparecen en la ecuacion de la velocidad, es decir, que el orden total de reacción será α+β+γ+...

Pero la cosa no es siempre así de sencilla... Las especies que aparecen en la ecuación experimental de la velocidad de reacción no tienen porqué ser reactivos o productos de ésta. Una velocidad de reacción puede ser función de la concentración de cualquier sustancia presente en el medio, tanto si se trata de un reactivo, un producto o sustancias que no aparecen en la estequiometría de la reacción (puede ser un producto intermedio, un catalizador, ... etc.). También son posibles órdenes de reacción negativos, es decir que la concentración de alguna especie aparezca dividiendo en la ecuación, y también existen ecuaciones de la velocidad de reacción mucho más complicadas que la ecuación escrita arriba, con dos o más términos en el segundo miembro de la ecuación.

Los órdenes parciales que respectan de las concentraciones de los reactivos tienen coincidencia con los coeficientes estequiométricos de las diferentes ecuaciones químicas. Sin embargo, se debe indicar que en un inicio no hay relación entre ellos.

La expresión para la ecuación de velocidad es:

Velocidad = K [A]^n[B]^m

De donde n y m se consiguen de manera experimental, y hacen referencia al orden parcial de la reacción del reactivo A y el reactivo B, siendo la suma de n y m la que determine el orden total de dicha reacción.

A la constante de proporcionalidad se le designa la letra K, y se la conoce como constante de velocidad. Esta suele ser la velocidad de la reacción cuando las concentraciones de los reactivos en su totalidad son la unidad, es decir, 1 mol/l.

La K, es específica para cada reacción, y es dependiente de la temperatura. Las unidades en las que se expresa K, están determinadas por el orden de la reacción en total, y se deben adaptar a las condiciones en las que la velocidad se exprese.

Para la determinación de la ecuación de velocidad en una reacción química, se debe investigar la dependencia que tiene la velocidad con respecto a la concentración de los reactivos que participan en la reacción, por lo que es necesario saber los órdenes parciales, y el valor de la constante de velocidad.

Una manera fácil de hallar la ecuación de velocidad es usar el método de la velocidad inicial, en el cual se determina la velocidad de la reacción al inicio de ésta. En el momento inicial de la reacción, las concentraciones de los reactivos se encuentra aún elevadas, y la velocidad instantánea es sencilla de medir con gran precisión. Esto consiste en variar la concentración de uno de los reactivos, manteniendo las concentraciones de los demás reactivos constantes, y así poder estudiar como varía o se modifica la velocidad.