Energía potencial elástica

La energía potencial elástica es energía almacenada que resulta de aplicar una fuerza para deformar un objeto elástico. La energía queda almacenada hasta que se quita la fuerza y el objeto elástico regresa a su forma original, haciendo un trabajo en el proceso. La deformación puede implicar comprimir, estirar o retorcer el objeto. Muchos objetos están diseñados específicamente para almacenar energía potencial elástica, por ejemplo:

• El muelle de un reloj de cuerda.
• Un arquero que estira su arco.
• Un trampolín doblado justo antes de que el clavadista brinque.
• La liga de hule de una resortera.
• Una pelota de goma, comprimida en el momento en el que choca con una pared de ladrillos.

Un objeto diseñado para almacenar energía potencial elástica usualmente tendrá un límite elástico alto. Sin embargo, todos los objetos elásticos tienen un límite para la carga que pueden soportar. Cuando la deformación va más allá del límite elástico, el objeto ya no vuelve a su forma original. En generaciones anteriores, los relojes de cuerda accionados por muelles en espiral eran accesorios populares. Hoy en día, no solemos usar teléfonos inteligentes de cuerda porque no existen materiales con un límite elástico suficientemente alto como para almacenar energía potencial elástica con la densidad de energía suficientemente alta.

¿Cómo podemos calcular la energía potencial elástica de un resorte ideal?

En nuestro artículo sobre elasticidad y ley de Hooke discutimos cómo la magnitud de la fuerza, 

$F$

$F$

F

, debida a un resorte ideal depende linealmente de la longitud, 

$\Delta x$delta, x

, que se ha comprimido o expandido,

$F = k\cdot \Delta x$

$F=k\cdot \Delta x$

F, equals, k, dot, delta, x

donde 

$k$

$k$

k

 es algún número positivo, que llamamos "constante del resorte". La fuerza del resorte es conservativa, y las fuerzas conservativas tienen energías potenciales asociadas a ellas. 

[¿Qué pasa con la dirección de la fuerza?]

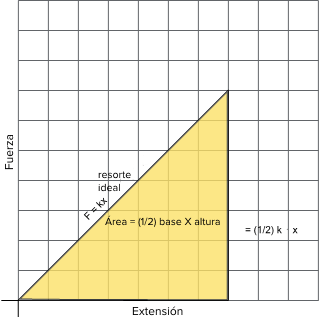
De la definición del trabajo sabemos que el área bajo una gráfica de fuerza vs. desplazamiento da el trabajo realizado por esa fuerza. La figura 1 muestra la gráfica de fuerza vs. desplazamiento de un resorte. Ya que el área bajo la curva es un triángulo, y ningún tipo de energía se pierde en un resorte ideal, podemos encontrar la energía potencial elástica 

$U$

$U$

U

 a partir del trabajo realizado:

$\begin{aligned}U &= \frac{1}{2} (\Delta x) \cdot k (\Delta x) \\ &= \boxed{\frac{1}{2} k (\Delta x)^2} \end{aligned}$

$\begin{array}{l}=\end{array}$

$\begin{array}{l}\genfrac{}{}{0ex}{}{1}{2}\end{array}$

(Δx)⋅k(Δx)

$\begin{array}{l}\\ =\boxed{\genfrac{}{}{0ex}{}{1}{2}{}^2}\end{array}$

Figura 1: el trabajo realizado por una fuerza sobre un resorte ideal.

Figura 1: el trabajo realizado por una fuerza sobre un resorte ideal.

Ejercicio 1: la suspensión de un camión tiene una constante de resorte de 

$5\cdot 10^4~\mathrm{N/m}$

$5\cdot 10$

${}^4$

 N/m

. Cuando no tiene carga, el camión se encuentra 0.8 m encima de la carretera. Cargado con mercancías, baja a 0.7 m por encima del suelo. ¿Cuánta energía potencial almacenan los cuatro resortes? 

[Solución]

$\Delta x$

delta, x

$\begin{aligned} U &= \frac{1}{2} k (\Delta x)^2 \\ &= \frac{1}{2} \cdot 5 \cdot 10^4~\mathrm{N/m} \cdot (0.1~\mathrm{m})^2 \\ &= 250~\mathrm{J}/\mathrm{resorte} \\ &= 1000~\mathrm{J} \end{aligned}$

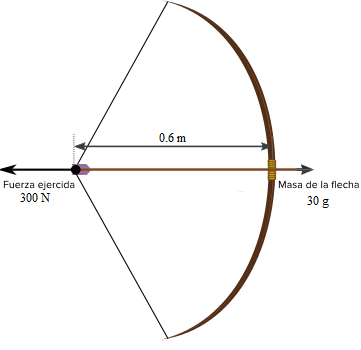
Ejercicio 2a: un arquero entrenado tiene la capacidad de estirar un arco con una fuerza de 300 N, extendiendo la cuerda 0.6 m hacia atrás. Suponiendo que el arco se comporta como un resorte ideal, ¿qué constante del resorte le permitiría al arquero hacer uso de toda su fuerza?

Un arco ten

$\begin{aligned}k &= \frac{F}{\Delta x}\\ &= \frac{300~\mathrm{N}}{0.6~\mathrm{m}} \\ &= 500 ~\mathrm{N/m} \end{aligned}$

Ejercicio 2b: ¿qué energía potencial almacena el arco cuando se estira

$\begin{aligned} U &= \frac{1}{2} k (\Delta x)^2 \\ &= \frac{1}{2} (500 ~\mathrm{N/m})\cdot (0.6~\mathrm{m})^2 \\ &= 90~\mathrm{J} \end{aligned}$

Ejercicio 2c: suponiendo que la flecha tiene una masa de 30 g, ¿a qué velocidad, aproximadamente, saldrá disparada.

$\frac{1}{2} m v^2 = U$start fraction, 1, divided by, 2, end fraction, m, v, start superscript, 2, end superscript, equals, U

$\begin{aligned}v &= \sqrt{\frac{2 U}{m}}\\ &= \sqrt{\frac{2\cdot 90~\mathrm{J}}{0.03~\mathrm{kg}}}\\ &\simeq 77.5~\mathrm{m/s}\end{aligned}$

Ejercicio 2d: supón que las medidas de una cámara de alta velocidad muestran que la flecha se mueve a una velocidad más lenta de lo previsto por la conservación de la energía. ¿Se está realizando algún trabajo que no hemos considerado.

¿Qué pasa con materiales elásticos reales?

En nuestro artículo sobre elasticidad y ley de Hooke discutimos cómo los resortes reales solamente obedecen la ley de Hooke para un rango particular de fuerza aplicada. Algunos materiales elásticos tales como ligas y plásticos flexibles pueden funcionar como resortes, pero a menudo presentan histéresis; esto significa que la curva de fuerza contra extensión sigue un camino diferente cuando el material es deformado en comparación a cuando regresa a su posición de equilibrio.

Afortunadamente, la técnica básica al aplicar la definición de trabajo que empleamos para un resorte ideal en general también funciona para materiales elásticos. Siempre podemos encontrar la energía potencial elástica a partir del área bajo la curva de la gráfica de fuerza vs. extensión, independientemente de la forma de la curva.

En nuestro análisis anterior, hemos considerado el resorte ideal como un objeto unidimensional. En realidad, los materiales elásticos son tridimensionales. Resulta que el mismo procedimiento sigue siendo válido. El equivalente a la curva de fuerza vs. distancia es la curva de esfuerzo vs. deformación. 

[¿Qué son el esfuerzo y la deformación?]

• $\mathrm{N/m^2}$
• $\Delta l$delta, l$l$l$\Delta l/l$delta, l, slash, l

Un material elástico tridimensional obedece ley de Hooke, donde

$\mathrm{Energía / volumen = \frac{1}{2} (esfuerzo \cdot deformación)}$

$\mathrm{E}\mathrm{n}\mathrm{e}\mathrm{r}\mathrm{g}$

$\acute{ı}$

$\mathrm{a}/\mathrm{v}\mathrm{o}\mathrm{l}\mathrm{u}\mathrm{m}\mathrm{e}\mathrm{n}=$

$\genfrac{}{}{0ex}{}{1}{2}\acute{\mathrm{o}}\mathrm{n})$

[¿Qué está pasando con las unidades en este caso?]

• $\Delta x / x$delta, x, slash, x
• $\mathrm{J\cdot m^{-1}}$$\mathrm{\frac{J\cdot m^{-1}}{m^2} = J/m^3}$

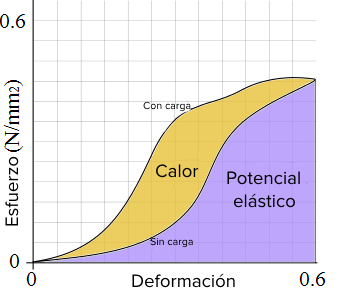
Ejercicio 3: la figura 3 muestra una gráfica de tensión vs. deformación para una banda de hule. Cuando está estirada (cargada), la curva toma el camino de arriba. Esto es porque, ya que la banda no es ideal, libera menos fuerza para una extensión dada al relajarse de nuevo (descargada). El área sombreada púrpura representa la energía potencial elástica para la máxima extensión. En amarillo se muestra la diferencia de área entre los dos casos: con carga y sin ella. Esto representa la energía que se pierde en forma de calor cuando la banda se estira y relaja.

Si la banda de hule tiene una longitud de 

$100~\mathrm{mm}$

$100\mathrm{m}\mathrm{m}$

, 

$10~\mathrm{mm}$

 de ancho y un grosor de 

$1~\mathrm{mm}$

, ¿cuánto calor se genera en la banda cuando se estira y se relaja de nuevo?