Energía potencial eléctrica

Energía potencial eléctrica

Al igual que cuando hablamos de la energía potencial gravitatoria estudiamos que un cuerpo que se encuentra a una determinada altura de la superficie de la Tierra adquiere una determinada cantidad de energía potencial provocada por la acción de la fuerza gravitatoria, un cuerpo cargado que sufre la acción de una fuerza eléctrica adquiere energía potencial eléctrica (Ep).

El trabajo realiza

do por la fuerza eléctrica para trasladar una carga desde un punto A a otro B se puede expresar de la siguiente forma:

W

e(A→B) 

=

∫

BA

F

→

e

d

l→

=−Δ

E

p

=−(

E

pB

−

E

pA

)

Esta expresión determina que sólo es posible calcular diferencias de energía (ΔEp) y la energía potencial en un punto es siempre un valor relativo con respecto a otro, sin embargo para hablar de un valor absoluto se utiliza como referencia un punto situado en el infinito. Dado que a esa distancia no existe fuerza eléctrica que atraiga o repela las cargas, la energía potencial eléctrica allí es nula. Por tanto, aplicando esta consideración obtenemos que:

W

e(∞→A) 

=

∫

A∞

F

→

e

d

l→

=−Δ

E

p

=−(

E

pA

−

E

p∞

)=−

E

pA

Tal y como estudiamos en el apartado de trabajo eléctrico, si sobre una carga actúa otra fuerza externa (a parte de la fuerza eléctrica), se cumple que:

W

e

=−

W

f

donde:

• We es el trabajo realizado por la fuerza eléctrica para moverlo desde A hasta B.
• Wf es el trabajo realizado por la fuerza externa para moverlo desde A hasta B.

Por esta razón, podemos definir el trabajo realizado por la fuerza externa para trasladar la carga desde el infinito hasta una posición A como:

W

f(∞→A) 

=−

W

e(∞→A) 

= 

E

pA

La energía potencial eléctrica de una carga situada en una posición A equivale al trabajo realizado por una fuerza externa para trasladar dicha carga desde el infinito hasta dicha posición A, o dicho de otra forma, el opuesto del trabajo realizado por la fuerza eléctrica para llevarla desde el infinito hasta A.

E

pA

=

W

f(∞→A) 

=−

W

e(∞→A) 

Energía potencial de un sistema de dos partículas

Si disponemos de dos cargas Q y q, el trabajo para aproximar q desde el infinito hasta un punto A próximo a Q se puede obtener aplicando la definición de trabajo entre dos puntos:

W

e(∞→A)

=

∫

A∞

F

→

e

d

l→

=

∫

A∞

F

e

dr =−K⋅Q⋅q⋅

∫

A∞1r2

dr ⇒

W

e(∞→A)

=−K⋅Q⋅q⋅

[−

1r

]

A∞

⇒

W

e(∞→A)

=−K⋅

Q⋅q

r

Sustituyendo por la definición de energía potencial:

E

pA

=K⋅

Q⋅q

r

La energía potencial eléctrica que posee una carga puntual q en presencia de otra carga puntual Q que se encuentran separadas cierta distancia r es:

E

p

=K⋅

Q⋅q

r

donde:

• Ep es la energía potencial eléctrica. En el S.I. se mide en Julios (J).
• Q y q son los valores de las dos cargas puntuales. En el S.I. se miden en Culombios (C).
• r es el valor de la distancia que las separa. En el S.I. se mide en metros (m).
• K es la constante de la ley de Coulomb. Para el vacío su valor es aproximadamente 9·109 N·m2/C2utilizando unidades en el S.I.

Como ya hablamos en el apartado de trabajo eléctrico, este es el trabajo que realizan las fuerzas eléctricas y no debemos confundirlo con el trabajo que puede realizar una fuerza externa en contra de las fuerzas eléctricas para intentar aproximar dos cuerpos cargados con el mismo signo (que apriori intentarán separarse) o alejar dos cuerpos cargados con distinto signo (que apriori intentarán unirse). El trabajo que realiza dicha fuerza (Wf) se relaciona con el trabajo eléctrico (We) y la energía potencial eléctrica de la siguiente forma :

W

e

=−

W

f

=−Δ

E

p

A continuación, vamos a estudiar que esta relación se cumple en los dos casos comentados anteriormente.

Cargas con distinto signo

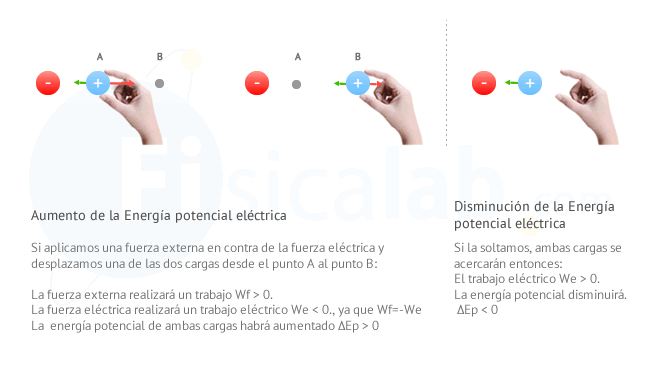
Imagina dos cargas fijas, una positiva y otra negativa. En principio, dado que se tratan de cargas con distinto signo en cada una de ellas aparecerá una fuerza de atracción hacia la otra. Imagina nuevamente que una de ellas se encuentra en un punto A y que podemos cogerla con la mano y situarla hasta un punto B más alejado. Al hacer esto:

• Si aplicas la definición de trabajo, dado que el desplazamiento se produce en la dirección y sentido de la fuerza externa, el trabajo que realiza esta fuerza (Wf) será positivo (Wf>0).
• Como el desplazamiento se produce en sentido contrario a la fuerza eléctrica, el trabajo eléctrico será negativo (We<0).
• Si aplicas la definición de energía potencial eléctrica, podrás comprobar que la energía en B es mayor que en A, por tanto (ΔEp>0).

En resumidas cuentas, el trabajo que realiza la fuerza externa al alejarlas, hace que las cargas adquieran energía potencial. Si ahora la soltamos, la fuerza eléctrica se encargará de acercarlas realizando un trabajo que consumirá parte o toda la energía potencial que poseen.

Cargas del mismo signo

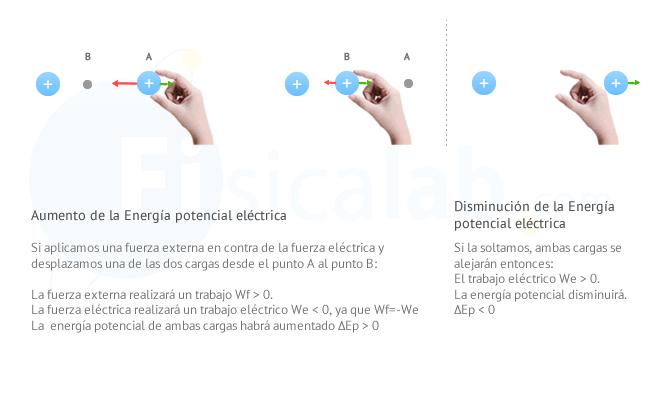
Ahora, imagina dos cargas fijas del mismo signo (positiva o negativa). En principio, dado que se tratan de cargas con signos iguales en cada una de ellas aparecerá una fuerza de repulsión en contra de la otra. Imagina nuevamente que una de ellas se encuentra en un punto A y que podemos cogerla con la mano y situarla hasta un punto B más cercano. Al hacer esto, como en el caso anterior:

• Si aplicas la definición de trabajo, dado que el desplazamiento se produce en la dirección y sentido de la fuerza externa, el trabajo que realiza esta fuerza (Wf) será positivo (Wf>0).
• Como el desplazamiento se produce en sentido contrario a la fuerza eléctrica, el trabajo eléctrico será negativo (We<0).
• Si aplicas la definición de energía potencial eléctrica, podrás comprobar que la energía en B es mayor que en A, por tanto (ΔEp>0).

El trabajo que realiza la fuerza externa al acercarlas, hace que las cargas adquieran energía potencial. Si ahora la soltamos, la fuerza eléctrica se encargará de alejarlas realizando un trabajo que consumirá parte o toda la energía potencial que poseen.

Fíjate que tal y como indicamos en la fórmula inicial, cuando se aplica la fuerza externa, el signo del trabajo del campo eléctrico es exactamente el contrario al del trabajo realizado por la fuerza eléctrica y al de la diferencia de energía potencial.

Energía potencial eléctrica de un sistema de más de dos partículas

Si en lugar de poseer dos cargas puntuales, disponemos de más cargas, podemos calcular la energía potencial del sistema sumando algebraicamente  la energía potencial eléctrica entre cada pareja de cargas. Por ejemplo, si disponemos de tres cargas q1, q2 y q3 la energía potencial eléctrica del sistema se obtiene por medio de la siguiente expresión:

E

p

=K⋅

q

1

⋅

q

2

r1,2

+K⋅

q

1

⋅

q

3

r1,3

+K⋅

q

2

⋅

q

3

r2,3

La energía potencial de un sistema formado por varias cargas puntuales equivale al trabajo necesario que debería realizar una fuerza exterior para ensamblar las cargas en esas posiciones trayéndolas desde el infinito.

Energía potencial eléctrica y energía cinética

Si dos o más cargas puntuales se enceuentran sometidas únicamente a la fuerza eléctrica, la energía total del sistema es siempre la misma (permanece constante). Esto es debido a que la fuerza eléctrica es una fuerza conservativa. ¿Que consideraciones tiene esto?. En primer lugar, que la suma de la energía cinética y la energía potencial de el sistema es independiente del punto en que se encuentre, por tanto entre dos puntos A y B se cumple que:

E

cA

+

E

pA

=

E

cB

+

E

pB

De igual forma, si disminuye la energía cinética, aumentará la energía potencial y viceversa. De esta forma también se cumple que:

Δ

E

c

+Δ

E

p

=0 ⇒

Δ

E

c

=−Δ

E

p

=

W

e(A→B)