Aceleración Angular

Aceleración Angular

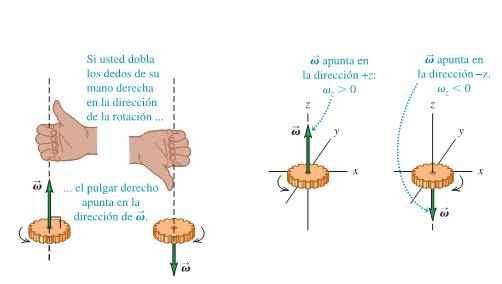
La aceleración angular es la variación que afecta a la velocidad angular tomando en consideración una unidad de tiempo. Se representa con la letra griega alfa, α. La aceleración angular es una magnitud vectorial; por lo tanto, consta de módulo, dirección y sentido.

La unidad de medida de la aceleración angular en el Sistema Internacional es el radián por segundo al cuadrado. De este modo, la aceleración angular permite determinar cómo varía la velocidad angular a lo largo del tiempo. A menudo se estudia la aceleración angular ligada a los movimientos circulares uniformemente acelerados.

De este modo, en un movimiento circular uniformemente acelerado el valor de la aceleración angular es constante. Por el contrario, en un movimiento circular uniforme el valor de la aceleración angular es cero. La aceleración angular es la equivalente en el movimiento circular a la aceleración tangencial o lineal en el movimiento rectilíneo.

De hecho, su valor es directamente proporcional al valor de la aceleración tangencial. Así cuando mayor es la aceleración angular de las ruedas de una bicicleta, mayor es la aceleración que esta experimenta.

Por tanto, la aceleración angular está presente tanto en las ruedas de una bicicleta como en las ruedas de cualquier otro vehículo, siempre y cuando se produzca una variación de la velocidad de giro de la rueda.

Del mismo modo, la aceleración angular también está presente en una noria, ya que esta experimenta un movimiento circular uniformemente acelerado cuando inicia su movimiento. Por supuesto, también puede encontrarse la aceleración angular en un tiovivo.

¿Cómo calcular la aceleración angular?

En general, la aceleración angular instantánea se define a partir de la siguiente expresión:

α = dω / dt

En esta fórmula ω es el vector velocidad angular, y t es el tiempo.

La aceleración angular media se puede calcular igualmente a partir de la siguiente expresión:

α = ∆ω / ∆t

Para el caso particular de un movimiento plano, sucede que tanto la velocidad angular como la aceleración angular son vectores con dirección perpendicular al plano del movimiento.

Por otra parte, el módulo de la aceleración angular se puede calcular a partir de la aceleración lineal por medio de la siguiente expresión:

α = a /R

En esta fórmula a es la aceleración tangencial o lineal; y R es el radio de giro del movimiento circular.

Movimiento circular uniformemente acelerado

Como ya se ha mencionado anteriormente, la aceleración angular está presente en el movimiento circular uniformemente acelerado. Por este motivo, es interesante conocer las ecuaciones que gobiernan dicho movimiento:

ω = ω₀ + α ∙ t

θ = θ₀ + ω₀ ∙ t + 0,5 ∙ α ∙ t²

ω² = ω₀² + 2 ∙ α ∙ (θ – θ₀)

En estas expresiones θ es el ángulo recorrido en el movimiento circular, θ₀ es el ángulo inicial, ω₀ es la velocidad angular inicial, y ω es la velocidad angular.
Torque y aceleración angular
En el caso de un movimiento lineal, de acuerdo a la segunda ley de Newton se requiere una fuerza para que un cuerpo adquiera una determinada aceleración. Esa fuerza es el resultado de multiplicar la masa del cuerpo y la aceleración que ha experimentado el mismo.

Sin embargo, en caso de un movimiento circular, la fuerza que se requiere para impartir aceleración angular se llama torque. En definitiva, el torque se puede entender como una fuerza angular. Se denota con la letra griega τ (pronunciada “tau”).

De igual modo, se debe tener en cuenta que en un movimiento de rotación, el momento de inercia I del cuerpo realiza el papel de la masa en el movimiento lineal. De esta forma, el torque de un movimiento circular se calcula con la siguiente expresión:

τ = I α

En esta expresión I es el momento de inercia del cuerpo respecto al eje de rotación.

Ejemplos

Primer ejemplo

Determine la aceleración angular instantánea de un cuerpo que se mueve experimentando un movimiento de rotación, dada expresión de su posición en la rotación Θ (t) = 4 t³ i. (Siendo i el vector unitario en la dirección del eje x).

Igualmente, determine el valor de la aceleración angular instantánea cuando han transcurrido 10 segundos del inicio del movimiento.

 Solución

A partir de la expresión de la posición se puede obtener la expresión de la velocidad angular:

ω (t) = d Θ / dt = 12 t²i (rad/s)

Una vez calculada la velocidad angular instantánea, se puede calcular la aceleración angular instantánea en función del tiempo.

α (t) = dω / dt = 24 t i (rad/s²)

Para calcular el valor de la aceleración angular instantánea cuando han transcurrido 10 segundos, únicamente es necesario sustituir el valor del tiempo en el resultado anterior.

α (10) = = 240 i (rad/s²)

Segundo ejemplo

Determine la aceleración angular media de un cuerpo que experimenta un movimiento circular, sabiendo que su velocidad angular inicial era de 40 rad/s y que transcurridos, 20 segundos, ha alcanzado la velocidad angular de 120 rad/ s.

Solución

A partir de la siguiente expresión se puede calcular la aceleración angular media:

α = ∆ω / ∆t

α = (ω_f – ω₀) / (t_f – t₀ ) = (120  – 40 )/ 20 = 4 rad/s

Tercer ejemplo

¿Cuál será la aceleración angular de una noria que comienza a moverse con un movimiento circular uniformemente acelerado hasta que, al cabo de 10 segundos, alcanza la velocidad angular de 3 revoluciones por minuto? ¿Cuál será la aceleración tangencial del movimiento circular en ese periodo de tiempo? El radio de la noria es de 20 metros.

Solución

En primer lugar, es necesario transformar la velocidad angular desde revoluciones por minuto a radianes por segundo. Para ello se lleva a cabo la siguiente transformación:

ω_f = 3 rpm = 3 ∙ (2 ∙ ∏) / 60 = ∏ / 10 rad/s

Una vez realizada tal transformación, es posible calcular la aceleración angular dado que:

ω = ω₀ + α ∙ t

∏ / 10  = 0 + α ∙ 10

α = ∏ / 100 rad / s²

Y la aceleración tangencial resulta de operar la siguiente expresión:

α = a /R

a = α ∙ R = 20 ∙ ∏ / 100 = ∏ / 5  m / s²