La Energía Potencial Gravitatoria
Es la energía que posee un objeto debido a su posición en un campo gravitatorio y representa el potencial que un objeto tiene para realizar trabajo como resultado de estar ubicado en una posición particular dentro de ese campo gravitatorio. Un ejemplo, si suponemos el campo gravitatorio de la tierra, una pelota sobre su superficie no tiene energía potencial gravitatoria, pero si la elevamos a una altura de 3 metros, el trabajo necesario para elevarla respecto a la superficie de la tierra, es la energía potencial gravitatoria que tendrá la pelota a esa altura de 3 metros. Como ves la Energía Potencial Gravitatoria de la pelota depende de su posición y representa el trabajo realizado para colocarla en esa posición.
Pero...expliquemos un poco mejor todo esto para entenderlo.
Lo primero que tenemos que recordar es la Ley de Newton sobre la Ley de Gravitación Universal o Fuerza de Gravedad. Esta ley nos dice que 2 cuerpos cualquiera en el espacio, solo por el hecho de tener masa, se atraen con una fuerza llamada "fuerza de gravedad". Más adelante veremos más desarrollada esta expresión, de momento con esto nos vale para entender la Energía Potencial Gravitatoria cerca de la Superficie Terrestre.
La Energía Potencial Gravitatoria es aquella que está relacionada con la gravedad. En el caso de la Tierra, con la gravedad de la Tierra.
La masa de la tierra y la masa de nuestro cuerpo (o dos masas cualquiera) se atraen por la llamada fuerza gravitatoria o de gravedad, por eso estamos pegados a la tierra y tenemos un peso, nuestra masa por la fuerza con la que la tierra nos atrae (g = gravedad). Lógicamente al ser mucho mayor la masa de la tierra que la nuestra, solo notamos la atracción nosotros, no la tierra, ya que su masa es tan grande que la fuerza que nosotros hacemos sobre ella ni la nota.
Cuando un astronauta sale al espacio, la fuerza de atracción de la tierra sobre él va disminuyendo a medida que se aleja de la Tierra (mayor distancia que los separa). Cuando se encuentra ya demasiado lejos, la Tierra deja de atraerlo y en ese instante el astronauta pierde completamente su peso, aunque sigue teniendo masa, y se sitúa en lo que llamamos gravedad cero o ausencia de gravedad. En ese momento deja de estar bajo la influencia del campo de gravedad de la tierra porque se salió del campo gravitatorio de la tierra (zona de atracción). La zona donde un cuerpo se ve atraído por la tierra se llama campo gravitatorio de la tierra. Si hablamos de la Luna, sería la zona de atracción de la luna hacia otros cuerpos, y así para cualquier otro planeta del Universo.
Según lo visto, un campo gravitatorio es una región de espacio donde dos cuerpos con masa se atraen (fuerza). El más famoso para nosotros es el Campo Gravitatorio de la Tierra y la llamada fuerza de gravedad de la tierra, que es la fuerza con que la Tierra atrae a los cuerpos dentro de su campo gravitatorio.
El uso más común de la energía potencial gravitatoria es para objetos cercanos a la superficie de la Tierra donde se puede suponer que la aceleración gravitacional (aumento de velocidad según van cayendo los cuerpos) es constante y de valor aproximadamente g = 9.8 m/s2. Esta suposición hace que el campo gravitatorio cercano a la superficie de la Tierra sea uniforme. Luego veremos como para grandes distancias, esto no es cierto.
El cero de energía potencial gravitatoria se puede elegir en cualquier punto (como la elección del cero de un sistema de coordenadas). Una vez elegido el punto donde es 0, la energía potencial a una altura h por encima de ese punto, es igual al trabajo que se requeriría para elevar el objeto hasta esa altura. Lo normal es elegir el suelo como punto donde suponemos la Energía Potencial Gravitatoria de valor 0.
La fórmula quedaría:
Epg = Peso x Altura = (masa x gravedad tierra) x h = mgh
La energía potencial gravitatoria, Epg, se miden en julios (J), la masa, m se mide en kilogramos (kg), la aceleración de la gravedad, g, en metros/segundo-cuadrado (m/s2) y la altura, h, en metros (m). Recuerda que la altura h, es la medida respecto al cero de referencia elegido. Más abajo tienes la demostración de esta fórmula.
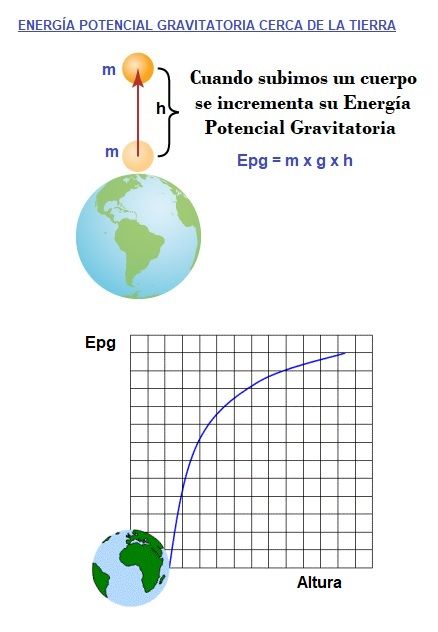
Una vez que desarrollamos el trabajo para subir el objeto a la altura h, si ahora soltamos el objeto volvería a caer hacia el suelo y la energía potencial gravitatoria que posee se iría transformado en energía cinética, aumentando su velocidad, a medida que disminuye su h. Cuando h es 0, es decir en el punto de referencia, su Energía Potencial volvería a ser 0. Para saber más sobre esto ver: Energía Cinética y Potencial.
Veamos un ejemplo sencillo:
Calcula la energía potencial gravitatoria que almacena una caja de 50 kg al ser elevada a una altura de 12 m por encima del nivel del piso.
Datos: Epg = ?, m = 50 kg, h = 12 m, g = 9,8 m/s2
Ep = m x g x h
Reemplazas los datos en la fórmula:
Ep = 50 kg x 9,8 m/s2 x 12 m.
Ep = 5880 J. La energía potencial gravitatoria que almacena la caja es de 5880 J.
Si ahora soltamos la caja, los 5880 Julios se irían transformando en velocidad (energía cinética). Según disminuye su altura, iría disminuyendo su Epg, hasta que alcanza el suelo que sería Epg = 0 Julios, porque toda se transformó en cinética (velocidad) justo en el momento que toca el suelo.
En realidad, la energía potencial gravitatoria cerca de un planeta es negativa, ya que la separación de dos masas, bueno en nuestro caso solo una la del objeto que separamos de la Tierra, no es un proceso espontáneo, si no que requiere efectuar un trabajo en contra de la fuerza de atracción del Planeta.
Este potencial negativo es indicativo de un "estado unido". Una vez que una masa está cerca de un cuerpo grande (planeta), queda atrapada hasta que algo pueda proporcionar suficiente energía para permitir que escape.
Nota: "g" en la tierra es 9,8 m/s2 y muchas veces se puede aproximar por 10. Para otro planeta este valor es diferente
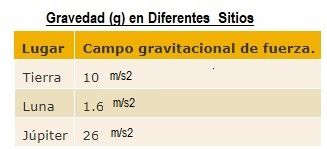
En la Tierra, una bola de masa de 0,5 kg se golpea hacia arriba. ¿Cuánto Epg tiene en su punto más alto a 6 m del suelo?
Epg = 0.5 x 10 x 6 = 30 J
En la Luna, si a la misma bola se le diera la misma cantidad de Epg, ¿Qué altura alcanzaría por encima de la superficie?
h = Epg / (m x gluna) = 30 / (0.5 x 1.6) = 37.5 m
El peso de un objeto es el tamaño de la fuerza de gravedad que tira del objeto hacia abajo. Un astronauta pesa más en la Tierra que en la Luna, ya que la gravedad de la Tierra es más fuerte que la de la Luna, sin embargo su masa siempre es la misma (a no ser que le cortemos un trozo de cuerpo). Peso = masa x g.
En la Tierra, ¿cuál es el peso de una persona cuya masa es de 120 kg? ¿Cual sería su peso en la Luna?
Si si, el peso no se mide en Kg se mide en Newtons, aunque la gente diga Kg, físicamente esta mal expresado. Puedes saber más aquí: Masa y Peso.
Puedes ver más ejercicios sobre la energia potencial resueltos en el siguiente enlace: Ejercicios Energia Potencial, y sobre caida libre de los cuerpos aqui: Problemas de Caida Libre.
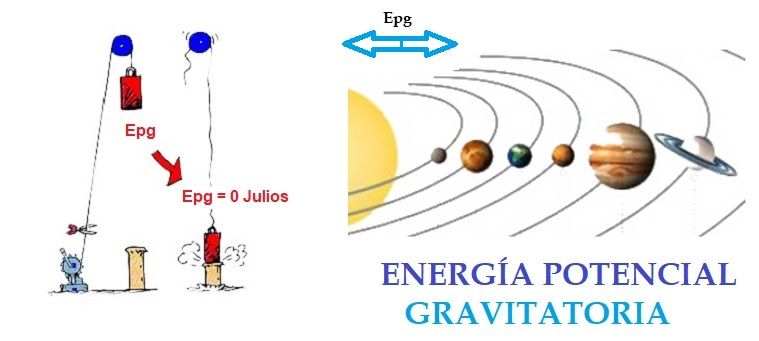
Energía Potencial Gravitatoria en Distancias Muy Grandes (Campos No Uniformes)
En estos casos se aplica la Ley de Newton sobre la Gravitación Universal.
"Dos cuerpos cualquiera se atraen entre si con una fuerza directamente proporcional al producto de sus masas e inversamente proporcional al cuadrado de la distancia que los separa. La fuerza de atracción de los dos cuerpos tiene la dirección de la recta que une los cuerpos". Dicha fuerza se conoce como fuerza de la gravedad o fuerza gravitacional y se expresa de la forma:
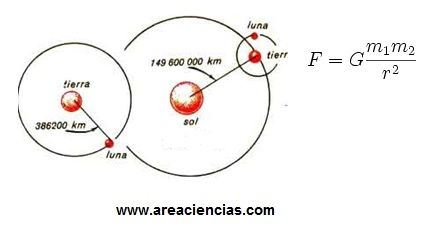
Las masas de los 2 cuerpos en el Universo serían m1 y m2, y r sería la distancia que las separa. La G es la llamada "constante gravitacional universal", una constante que tiene el mismo valor en todo el universo.
G = 6,674 x 10-11
En la imagen puedes ver como el Sol atrae a la Tierra, y la Tierra atrae a la Luna, por eso estamos girando unos alrededor de los otros formando una órbita.
Cuando hablemos de calcular la Energía Potencial Gravitatoria de algún cuerpo en el Espacio, y cuya distancia a la Tierra o cualquier otro planeta sea muy grande (campo gravitatorio no uniforma), entonces debemos aplicar esta fórmula que es válida para todo el universo. Pero....¿Cómo calculamos la Epg en estos casos?
Cuando tratamos con la energía potencial gravitatoria en grandes distancias, normalmente elegimos la ubicación de nuestro punto 0, en un punto que puede parecer contrario a la intuición. Colocamos el punto cero de energía potencial gravitatoria a una distancia "r" del infinito. ¿Por qué en el infinito?
Fíjate que cuando "r" se hace muy muy grande, la fuerza gravitacional de atracción (Newton) tiende rápidamente hacia cero (en la fórmula está dividiendo la distancia r). Un divisor (r) muy grande hará que el resultado de la formula sea 0. Es decir, para que en esa fórmula la fuerza de atracción sea cero, solo se cumplirá cuando los dos cuerpos estén situados en el infinito, r=∞, y ese es nuestro punto de partida donde Epg = 0.
Cuando estás cerca de un planeta, estás efectivamente atado al planeta por la gravedad y necesitas mucha energía para escapar. ¿Cuando escaparías de su fuerza de atracción? Estrictamente, solo escaparías cuando la fuerza de atracción fuera 0, o lo que es lo mismo, cuando r es igual a infinito.
En la realidad, como también influyen las masas (m1 x m2), hay una distancia en la que la fuerza de atracción es casi 0, y es hasta donde se supone que estaríamos atrapados por el planeta, o lo que es lo mismo, su campo gravitatorio (zona de atracción).
Por ejemplo, para una nave espacial que abandona la Tierra, se puede decir que esto ocurre a una altura de aproximadamente 5 x 107 metros sobre la superficie de la Tierra. A esa altura, la aceleración debida a la gravedad ha disminuido a aproximadamente al 1% de su valor en la superficie.
¿Por qué Cerca de la Superficie de la Tierra Epg = mgh?
Aquí tienes la demostración.
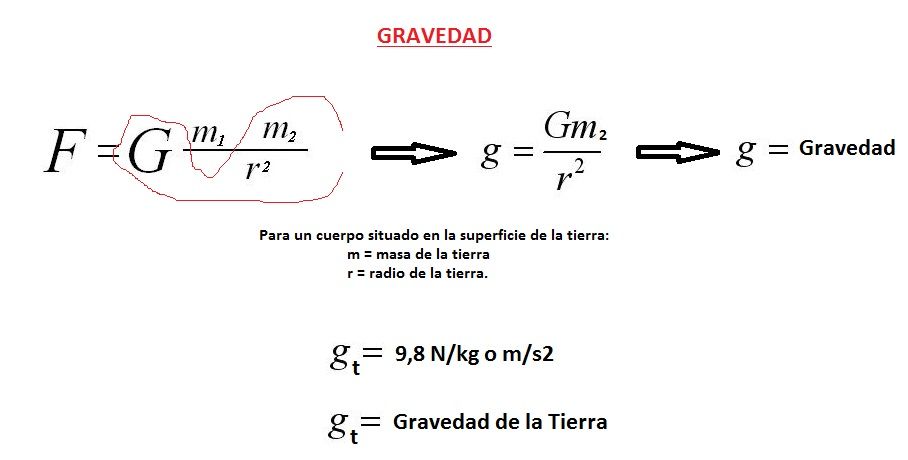
En la fórmula principal, si queremos calcular la fuerza de atracción, por ejemplo que ejerce la tierra sobre una persona en su superficie, resulta que para cualquier objeto situado en cualquier parte de la superficie de la tierra, G, la m2 (masa de la tierra) y r el radio de la tierra (el cuerpo está en su superficie), tienen siempre los mismos valores. OJO suponiendo que la tierra es una esfera perfecta. Estos valores, también serían constantes en el supuesto de hablar de la luna u otro planeta, pero diferente para cada uno, ya que tienen diferentes masas y radios.
Si agrupamos esos valores (G, m2 y r) en una constante llamada g (minúscula) a esa g es a lo que llamamos gravedad y como puedes ver depende del valor de m2, es decir, de la masa del cuerpo grande y de su radio. Por eso en la tierra tiene un valor siempre igual (m2 = masa de la Tierra), pero en la luna otro diferente, ya que sus masas y radios no son iguales.
Ahora para calcular el Trabajo necesario para subir un cuerpo desde la superficie de la tierra necesitamos multiplicar esos valores por la distancia a la que lo subimos, por eso sería; Epg = m x g x h.
Einstein y La Gravedad
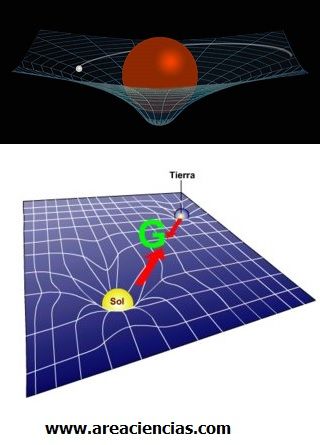
Para acabar, decir que mucho después de Newton, Einstein dijo una teoría sobre la gravedad de los cuerpos en el espacio cuando están separados por grandes distancias (por ejemplo para los planetas), teoría que es la aceptada hoy en día, que cambia el concepto pero no los cálculos.
Teoría de Einstein sobre la Gravedad: la gravedad, cuya presencia estaba presente en todos lados donde existiera un cuerpo, no se trataba de una fuerza en sí, sino de geometría, la presencia de un cuerpo en el espacio deformaba el “espacio-tiempo” y era esta deformación lo que atraía a los cuerpos entre ellos. Para saber más: Ley de la Gravedad Según Einstein.
No hay comentarios.:
Publicar un comentario