MASA Y FUERZA

MASA Y FUERZA

Las leyes de Newton reposan sobre las definiciones básicas de masa y fuerza. Sin embargo, examinando dichas leyes con espíritu crítico, es fácil ver que las definiciones realizadas por Newton de estos conceptos adolecen de algunas deficiencias.

La definición de fuerza (definición IV, Aptdo. 1.4) es claramente circular con la primera ley. En efecto, se podría entender ésta como una definición de fuerza, obviando la definición anterior dada por Newton. Aún aceptando esto, tampoco se puede considerar esta ley como una definición precisa de fuerza, ya que no proporciona una manera de medir su valor de forma cuantitativa. En realidad tan sólo se podría deducir de la primera ley cuándo la fuerza es nula o cuándo no lo es. La segunda ley sin embargo sí se puede interpretar como una definición cuantitativa de fuerza, pero esto la privaría a su vez de su consideración como principio.

En cuanto a la definición de masa (definición I, Aptdo. 1.4), Newton la refiere a la densidad (r) y volumen (V ) que integran un cuerpo (M = rV ).

¿Cuál sería entonces la definición de densidad? Es difícil aceptar que la densidad sea un concepto más fundamental que el de masa.

Un procedimiento aparentemente más riguroso para definir la masa es el debido a E. Mach9 (1858-1916), que resumimos a continuación.

Sean dos partículas, a y b, formando un sistema binario aislado. Expresando la segunda ley de Newton para la partícula a:

maaa = Fab;

donde Fab es la fuerza ejercida sobre a por b. Análogamente para b,

mbab = Fba = - Fab;

por la 3.a ley de Newton. Así,

maaa = -mbab;

y empleando los módulos de las aceleraciones aa y ab,

mb/ma = - aa/ab

Suponiendo la masa ma como valor de referencia o definición de unidad de masa, este procedimiento nos permite medir la masa de cualquier partícula b a partir de la medición de las aceleraciones ab y aa. Aunque aquí, por clarificar la explicación, se ha llegado a esta definición partiendo de las leyes de Newton, sería posible considerarla como definición básica de masa, para comprobar posteriormente que, efectivamente, es consistente con las leyes de Newton.

De esta forma, con el espíritu crítico mencionado, cabría considerar las leyes primera y segunda de Newton como definiciones de fuerza, con lo que la única ley que expresa un postulado básico de la mecánica sería la ley tercera. Según Mach por tanto, es la ley tercera de Newton (principio de acción y reacción) la que reviste mayor importancia en la axiomática de la mecánica clásica.

En relación con esta última ley, puede ser objeto de cierta polémica la consecuencia implícita de existencia de acciones a distancia, es decir acciones que se propagan de manera instantánea (con velocidad infinita). En efecto, si se suponen dos cuerpos alejados entre sí con fuerzas de interacción centrales (dirigidas según la recta que las une), y uno de ellos sufre un cambio de posición, la ley de acción y reacción obligaría a que la fuerza de reacción sobre la otra partícula modificase su dirección de manera instantánea10.

En la realidad física parece que no existen tales interacciones instantáneas; respondiendo a ello la teoría de la relatividad restringida establece un límite a la velocidad de propagación de las interacciones, que es la velocidad de la luz en el vacío (c). Esto origina una cierta inexactitud de la mecánica clásica, error que sin embargo es muy pequeño para las fuerzas gravitatorias o elásticas en objetos «cotidianos.»

Conviene observar también que de la tercera ley se pueden hacer dos enunciados. En su forma débil, ciñéndose estrictamente al enunciado Newtoniano, establece que las fuerzas son iguales en magnitud y dirección y de sentido opuesto. Sin embargo, no presupone que tengan la misma dirección que la recta que une a las dos partículas sobre las que actúan. En el caso en que sí se verifique esta última hipótesis más restrictiva, se dice que se cumple el principio de acción y reacción en su forma fuerte, siendo las fuerzas centrales. En numerosos casos prácticos se verifican ambos enunciados del principio de acción y reacción, como son las fuerzas gravitatorias, elásticas, o electrostáticas. Sin embargo, existen fenómenos importantes en los que no se verifica en ninguna de sus dos formas. Estos casos corresponden a fuerzas que dependen de la velocidad, ligadas por lo general a campos que se propagan con velocidad finita, como son las fuerzas electrodinámicas debidas a cargas en movimiento.

En resumen, podemos clasificar las fuerzas citadas esquemáticamente como sigue.

Fuerzas centrales

Están asociadas a campos que suponen una acción a distancia, propagándose por tanto de manera instantánea. Se trata de fuerzas dirigidas hacia las partículas que las originan, cumpliendo la tercera ley de Newton en su forma fuerte.

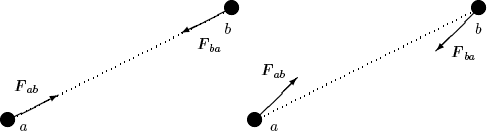
a) Fuerzas centrales    b) Fuerzas no centrales

Figura 1.2: Las fuerzas centrales están dirigidas según la recta que une los cuerpos, mientras que las fuerzas no centrales no verifican esta hipótesis, aún siendo iguales en magnitud y dirección y de sentido opuesto.

En mecánica clásica se admite esta hipótesis como adecuada para algunos de los tipos más usuales de fuerzas:

Fuerzas gravitatorias

La hipótesis de fuerza central e instantánea se considera adecuada para las mediciones en escalas usuales.

Sin embargo, para mediciones a escalas astronómicas o cosmológicas se trata de una hipótesis cuestionable. Sería más correcto interpretarlas mediante ondas de gravedad, que se propagan con la velocidad de la luz.

Fuerzas electrostáticas o magnetostáticas

De atracción o repulsión debidas a cargas eléctricas o magnéticas en reposo. Al igual que en el caso gravitatorio, de forma rigurosa para escalas astronómicas puede ser necesario considerar la transmisión de dichas fuerzas a través de ondas electromagnéticas.

Fuerzas elásticas

Ejercidas entre las partículas en contacto de un medio continuo. Por lo general, podría admitirse que son manifestaciones macroscópicas de las fuerzas electrostáticas entre las moléculas.

Fuerzas no centrales

Ocurren, por lo general, cuando las interacciones dependen de la velocidad, estando asociadas a campos que se propagan con velocidad finita:

Fuerzas Electromagnéticas

Cuando son debidas a cargas móviles pueden no cumplir tampoco el principio de acción y reacción en su forma débil.

Debe quedar claro que en este curso admitiremos la hipótesis de fuerzas centrales, por lo que será válido el principio de acción y reacción en su forma fuerte.

La definición de masa según el procedimiento de Mach arriba descrito no proporciona sin embargo un método viable para medirla. Sería prácticamente imposible aislar completamente un sistema binario y al mismo tiempo realizar mediciones. Una forma más práctica de medir la masa, aunque de forma indirecta, es con una balanza de resorte. En ésta lo que se mide directamente es el peso, o atracción gravitatoria hacia el centro de la Tierra. Basta dividir el peso (w) por la aceleración de la gravedad en la

superficie de la Tierra (g) para obtener la masa11:

9. E. Mach, The science of mechanics, traducción al inglés, Open Court, 1902.

10. Históricamente ha existido siempre, antes y después de Newton, una contestación a la posibilidad de tales acciones a distancia. Antiguamente se defendía que todo el espacio estaba lleno de una sustancia invisible, llamada _éter,_ vehículo transmisor de las fuerzas.
Este concepto sobrevivió a Newton, alcanzando su mayor predicamento dos siglos después para explicar el campo electromagnético, siendo la Teoría de la Relatividad la que acabó de desterrarlo.